Adaptive Multipoint Radius
The simplest version of Data Expansion we know is Maya Multipoint type particle. A simulation can be done with few numbers of particles (seed particle) that have multi points (second particle), so they look like many particles even though the second particles just follow seed particle, so usually it has a side effect where second particles look like groups.
uniform multipoints radius side effect
I tried to fix this problem using an adaptive radius of multipoint. My idea is to use the distance between the current particle and the nearest neighbor particle as a radius of multipoint radius.

B is the nearest neighbor particle of A, and ris the radius of A's multipoints radius.
adaptive multipoints radius test
To do this, I had to find the nearest neighbor particle of every particle. This is a very expansive process because I have to compare the distance of every particle and find the minimum value. If the number of particle is 100,000, comparing has to be done 10,000,000,000 times (100,000 * 100,000).
I tried this method in Maya using particle expression and Mel script and found it is impossible because once I increased the number of particle up to 10,000, I couldn’t see the result. Not only the process is expensive but also using Mel script in particle expression makes it much slow. (I was waiting about 10 minutes and gave up...)
So, I did some research and found if I can make a special data structure, which is kd-tree, nearest neighbor searching can be much faster. Also, Nearest Neighbor Searching is a well-known computer science issue, so there are some useful libraries.
Thread-safe Approximate Nearest Neighbor: http://compgeom.com/~stann/html/
This solution is even faster then regular nearest neighbor searching using kd-tree because this is Approximate Nearest Neighbor Searching. According to their explanation, it could be 10~100 times faster then the accurate nearest neighbor searching. I tested it with 100,000 particles and took less then 5 seconds. It gives me not just the nearest neighbor but the list of neighbors, so I can easily go to the second nearest neighbor and the others. I think I can use this solution for slicing through camera direction.
Improved Dots.so – Procedural Primitive DSO
I have written a very simple Procedural Primitive DSO for my cloud project which just creates 10 points in given position. I have added little more features.
The major change is the distribution of the points. The previous version just used random position of x, y, z, so its over all shape was like a cube.

However, I needed sphere-like shape. I have also used in_sphere() random function for my Python Helper Program project, At that time, I used Ivan Frohne’s python Random Number module, but for this project I had to do it in C. I tried to find some C library and found some C++ library instead of C.
So, I tried to make it myself. It’s not so simple to get uniformly distributed random positions in and on a sphere. There are two methods that I tried and didn’t want to use for on_sphere().
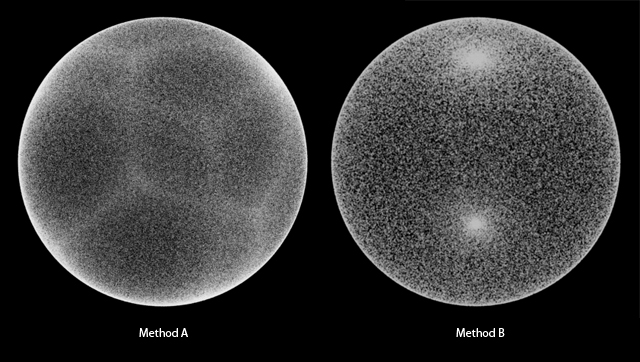
Method A is made by random numbers based on x, y, z value and normalize them, and we can still see the cube edges. Method B has a artifact where more particles are near both poles.
I did some research and found better method here.
http://mathworld.wolfram.com/SpherePointPicking.html

And this is the onSphereRandom() C code
For inSphereRandom() I used onSphereRandom() and converted it to Spherical Coordination System. Spherical Coordination System is another way to describe a position in 3D space which uses two angles and one distance from origin.
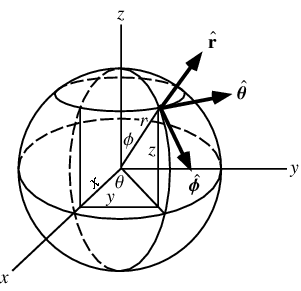
Source : http://mathworld.wolfram.com/SphericalCoordinates.html
First I converted the original x, y, z values to Spherical Coordination System (r, t, p) and put some random value into r (distance from origin) and then converted r, t, p to x, y, z again and got another artifact where more points are near the center.

Source : http://mathworld.wolfram.com/DiskPointPicking.html
It can be fixed simply using sqrt(random()) for r instead of using just random().

This is the inSphereRandom() C code.
And the new version of dots procedural primitive DSO.
Ri Filter Plug-in
The next step is converting the seed particles to the DSO. I used Ri Filter Plug-in to replace RiPoints procedure, which is particle in Maya, to RiDynamicLoad procedure, which is DSO call, in render time.
Ri Filter is an official way to do this kind of filtering. The reason Pixar provides this method is because many studios and individuals used to do this rib filtering by their own solutions, which the doc calls home-grown solutions. However, often time it was easy to spend more time for filtering rib then actual rendering. Using RiFilter eliminates the disk I/O time and also save the disk space, because everything is done in render time. RMS also now provides GUI for RiFilter.
However, the example C++ code in the Doc was not so simple to me. It took pretty much time to understand how it works. As well as, the example code does more then just “Hello World”.
This is the “Hello World” RiFilter that I made. It simply replaces RiCone to RiSphere and parses some parameters.
There are two header files for RiFilter. One is RiFilter.h and the other one is RiPlugin.h. RiPlugin.h provides the contact point to the renderer and use RiFilter.h as a dispatch table. RiFilter.h has almost all Ri procedure that ri.h has, so user can re-define Ri procedure using RiFilter.h.
There are two kinds of Ri procedure forms. One is RiXxxx() and the other one is RiXxxxV().
For example, to make
Surface “plastic” “Ks” [0.6] “Kd” [0.2]
We could use
RtFloat spec[1] = {0.6};
RtFloat diff[1] = {0.2};
RiSurface(“plastic”,”Ks”,spec,”Kd”,diff,RI_NULL);
However, since Ri procedure can have various number of parameters including primitive variables, ri.h provides the other form of RiSurface call.
RtFloat spec[1] = {0.6};
RtFloat diff[1] = {0.2};
RtToken keys[] = {“Ks”,”Kd”};
RtPointer vals[2];
vals[0] = (RtPointer)spec;
vals[1] = (RtPointer)diff;
RiSurfaceV(“plastic”,2,keys,vals);
This form can be more flexible when rib procedure has to get parameters dynamically in runtime.
RiFilter.h’s procedure form is the second form, so for this project I could parse additional custom primitive variables such as particle id for random seed or the adaptive multipoint radius that I made in Maya.
Points “P” [0 0 0 1 1 1] “constantwidth” [0.1] “id” [0 1] “multipointsRadius” [1 2] # <- green parts are the primitive variables that I want to export from Maya.
RMS provides a way to parse a custom attribute to a rib. If attribute name in Maya is rmanFxxx, xxx variable goes to the rib as a Float. Of course, we can do it for vector or integer using rmanVmyvector or rmanImyint.
One of the tricky parts was that I’m converting RiPoints to DSO call that makes again RiPoints. RiFilter works to readArchive and all procedurals, which means the RiPoints made by DSO is also filtered again. This is a kind of infinite loop. I spent so much time to find this problem and finally fixed it by comparing the number of parameters of RiPoints call, so if the RiPoints is from the original rib, it becomes RiReadDynamic, and if it is from DSO, it just makes points and terminates the process.
Expanded particle
Simulation with 300,000 particles and rendering with 9,000,000 particles
Render Time per frame : 13 min.
Memory usage: Average 1.2G
The seed particle - 300,000 points
I didn’t use the slice technique at this time because I still have long way to go for final solution. First of all, I have to solve the shadow problem where each slice has to cast and receive a shadow each other. Also a single frame has to be able to produce various numbers of images dynamically.